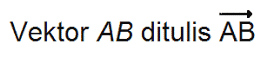Definisi Vektor, Cara Menggambar, Penjumlahan dan Penguranga Vektor serta Contoh Penyelesaian Soal Vekto

Simak Video Materi Besaran dan Resultan Vektor Berikut ini yah otakers!

Sumber: https://www.youtube.com/watch?v=GyWxS4MOJXU

Definisi Vektor adalah besaran yang memiliki nilai dan arah.

Contoh Vektor

Jika vektor merupakan sebuah besaran yang memiliki nilai dan arah maka contohnya adalah perpindahan, kecepatan, percepatan, gaya dan lain-lain.

Simbol Vektor

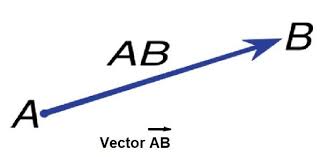
Simbol vektor ditulis menggunakan huruf kapital dan dicetak tebalatau miring dengan tanda panah diatasnya. Untuk simbol vector dapat anda lihat sebagai berikut.

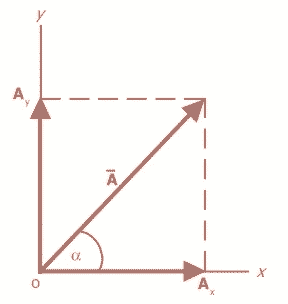
Pada bidang datar vektor mempunyai dua komponen yaitu pada sumbu X dan sumbu Y. Khusus untuk vektor yang segaris dengan sumbu X dan sumbu Y berarti hanya mempunyai 1 komponen.

Komponen Vektor adalah vector-vektor yang menyusun suatu vektor hasil atau yang disebut dengan Resultan Vektor.

Sehingga vektor bisa dipindahkan titik pangkalnya asalkan tidak berubah besar dan arahnya.

Oleh karena itu secara matematis vektor dapat dituliskan A = Ax+Ay dimana A adalah resultan dari komponen-komponenya berupa Ax dan Ay. (Perhatikan Gambar berikut ini).

Vektor Pada Bidang Datar

Penjumlahan Vektor

Penjumlahan vektor ialah operasi yang dilakukan untuk mencari sebuah vektor yang komponen vektornya tersebut merupakan penjumlahan dari kedua komponen vektor pembentuknya tersebut atau secara sederhana dapat dikatakan dengan mencari resultan dari dua vektor.

Vektor Segaris

Untuk vektor segaris, resultannya adalah : R = A + B + C + n dst

Vektor Tidak Segaris

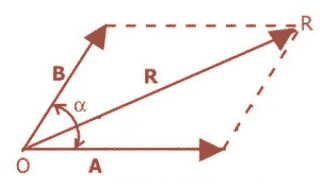
Jika sobat menemukan penjumlahan vektor tidak segaris seperti pada gambar 1 berikut ini.

Gambar 1

Jika anda menemukan soal penjumlahan vektor seperti pada gambar 1, maka berikut adalah bentuk rumus dan penyelesaiannya: (Perhatikan gambar 2)

Gambar 2

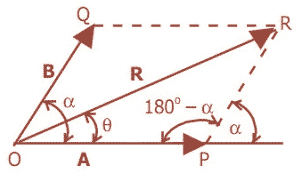
Penjelasan:

    Menurut aturan cosinus dalam segitiga,

    (OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) cos (180o – ?)

    (OR)2 = (OP)2 + (PR)2 – 2(OP)(PR) -(cos ?)

    (OR)2 = (OP)2 + (PR)2 + 2(OP)(PR) cos ?

    Jika OP = A, PR = B, dan Resultan ‘R’ = OR

    Maka didapat persamaan

    R2 = A2 + B2 + 2AB cos ?

    Rumus menghitung resultan vektornya

    R2 = A2 + B2 – 2AB cos ?

Nonton Juga Video Kita  : 

Belajar Fisika Mencari Nilai Dan Arah Resultan Vektor

Penjumlahan Vektor dengan cara Jajar Genjang (Pararelogram)

Penjumlahan vektor dengan cara jajar genjang merupakan cara yang dijelaskan di atas. Metode yang digunakan adalah dengan mencari diagonal jajar genjang yang terbentuk dari 2 vektor dan tidak ada pemindahan titik tangkap vektor.

Penjumlahan Vektor dengan Cara Segitiga

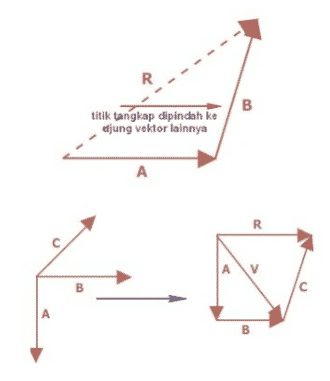
Penjumlahan vektor dengan cara segitiga yaitu dilakukan dengan pemindahan titik tangka vektor satu ke ujung vektor yang lainnya kemudian menghubungkan titik pangkal atau titik tangkap vektor pertama dengan titik ujung vektor kedua. Lihat ilustrasi gambar pada gambar 3.

Gambar 3

Pengurangan Vektor

Pengurangan vektor pada prinsip dasarnya adalah sama dengan operasi penjumlahan vector, akan tetapi yang membedakannya ialah salah satu dari vektor tersebut mempunyai arah yang berlawanan.

Contoh Pengurangan Vektor

Sebuah vektor A bergerak menuju ke arah timur dan vektor B bergerak menuju ke arah barat. Maka resultannya adalah R = A + (-B) = A – B.

Rumus Cepat Vektor

Untuk dapat mengerjakan vektor dengan mudah dan cepat maka berikut adalah Rumus Cepatnya!

    Jika ? = 00 maka R = V1 + V2

    Jika ? = 900 maka R = ?(V12 + V22)

    Jika ? = 1800 maka R = | V1 + V2 | –> nilai mutlak

    Jika ? = 1200 dan V1 = V2 = V maka R = V

Baca Juga : 

Vektor Posisi, Penyajian Vektor, dan Panjang Vektor

Vektor Matematika : Pengertian, Rumus, Operasi Vektor, Contoh Soal

Materi Besaran dan Resultan Vektor dalam Fisika Lengkap

Contoh Soal Vektor

Dua buah vektor dalam satu bidang berturut-turut besarnya adalah 8 satuan dan 6 satuan, kedua vektor tersebut bertitik tangkap sama serta mengapit sudut 30^o. Tentukanlah besar dan arah resultan vektor tersebut tersebut!

Jawaban:

R2 = A2 + B2 – 2AB cos ?

R = 82 + 62 + 2.6.8.cos 30

R = 64 + 36 + 96 0,5 ?3

R = 100 + 48?3