Contoh Soal dan Pembahasan Garis dan Sudut

Dengan mempelajari contoh soal di bawah ini Anda sudah punya bayangan bagaimana bentuk-bentuk soal yang keluar pada UN. Selain itu Anda juga bisa memprediksikan bentuk-bentuk soal yang akan keluar UN nantinya.
Contoh Soal 1
Perhatikan gambar di bawah ini

Besar ∠ABD adalah ….
A. 98°
B. 105°
C. 112°
D. 119°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠ABD dan ∠CBD merupakan sudut saling pelurus, maka:
∠ABD + ∠CBD = 180°
7x° + 5x° = 180°
12x° = 180°
x = 15°
∠ABD = 7x°
∠ABD = 7. 15°
∠ABD = 105°
Jadi, besar ∠ABD adalah 105° (Jawaban B)
Contoh Soal 2
Perhatikan gambar di bawah ini
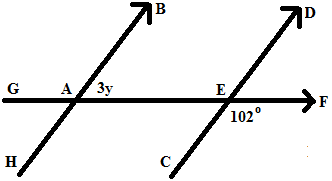
Nilai y adalah ….
A. 24°
B. 25°
C. 26°
D. 34°
(UN 2008/2009)
Penyelesaian:
Untuk menjawab soal ini Anda harus paham konsep hubungan antarsudut jika dua garis sejajar dipotong oleh garis lain. Dalam hal ini ∠CEF dan ∠EAH merupakan sudut sehadap, maka:
∠EAH = ∠CEF
∠EAH = 102°
Baca Juga :
Jenis Jenis Sudut Dan Pengertian Dan Contohnya
Penerapan Sudut dalam Kehidupan Sehari-hari
∠EAH + ∠BAE = 180° (sudut saling berpelurus)
102°+ 3y = 180°
3y = 180° - 102°
3y = 78°
y = 26° (Jawaban B)
Contoh Soal 3
Perhatikan gambar di bawah ini
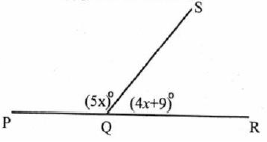
Besar pelurus sudut SQR adalah ….
A. 101°
B. 100°
C. 95°
D. 92°
(UN 2012/2013 paket 54)
Penyelesaian:
Perhatian** soal ini merupakan soal jebakan, banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini∠PQS dan ∠SQR merupakan sudut saling pelurus, maka:
∠PQS + ∠SQR = 180°
(5x)° + (4x+9)° = 180°
9x° + 9 = 180°
9x° = 171°
x° = 19°
Pelurus ∠SQR = ∠PQS
Pelurus ∠SQR = (5x)°
Pelurus ∠SQR = (5.19)°
Pelurus ∠SQR = 95° (Jawaban C)
Contoh Soal 4
Perhatikan gambar berikut

Besar sudut nomor 1 adalah 95°, dan besar sudut nomor 2 adalah 110°. Besar sudut nomor 3 adalah ….
A. 5°
B. 15°
C. 25°
D. 35°
(UN 2009/2010 paket 10)
Penyelesaian:
∠1 = ∠5 = 95° (sudut dalam berseberangan)
∠2 + ∠6 = 180° (saling berpelurus)
110° + ∠6 = 180°
∠6 = 70°
∠5 + ∠6 + ∠3 = 180°
95° + 70° + ∠3 = 180°
165° + ∠3 = 180°
∠3 = 15° (Jawaban B)
Contoh Soal 5
Perhatikan gambar
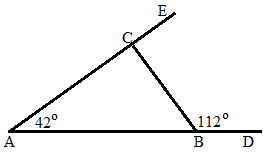
Besar ∠BCA adalah ….
A. 70°
B. 100°
C. 110°
D. 154°
(UN 2010/2011 paket 15)
Penyelesaian:
∠ABC + ∠CBD = 180° (saling berpelurus)
∠ABC + 112° = 180°
∠ABC = 68°
∠BCA + ∠ABC + ∠BAC = 180°
∠BCA + 68° + 42° = 180°
∠BCA + 110 = 180°
∠BCA = 70° (Jawaban A)
Contoh Soal 7
Perhatikan gambar di bawah ini

Besar ∠P3 adalah ….
A. 37°
B. 74°
C. 106°
D. 148°
(UN 2010/2011 paket 15)
Baca Juga :
Belajar Mengenal Sifat-Sifat Sudut Pada Dua Garis Sejajar Yang Dipotong
Menggambar Sudut yang besarnya kurang dari 180 ° dengan busur derajat
Rumus Sin Cos Tan Beserta Tabel, Rumus Identitas dan Relasi Sudut
Penyelesaian:
∠P2 = 74° (sudut luar berseberangan)
∠P2 + ∠P3 = 180° (saling berpelurus)
74° + ∠P3 = 180°
∠P3 = 106° (Jawaban C)
Contoh Soal 7
Perhatikan gambar di bawah ini

Besar pelurus sudut KLN adalah ….
A. 31°
B. 72°
C. 85°
D. 155°
(UN 2012/2013 paket 1)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠KLN dan ∠MLN merupakan sudut saling pelurus, maka:
∠KLN + ∠MLN = 180°
(3x + 15)° + (2x+10)° = 180°
5x° + 25° = 180°
5x° = 155°
x° = 31°
Pelurus ∠KLN = ∠MLN
Pelurus ∠KLN = (2x+10)°
Pelurus ∠KLN = (2.31 + 10)°
Pelurus ∠KLN = 72° (Jawaban B)
Contoh Soal 8
Perhatikan gambar di bawah ini

Besar penyiku ∠SQR adalah ….
A. 9°
B. 32°
C. 48°
D. 58°
(UN 2012/2013 paket 2)
Penyelesaian:
Perhatian** soal ini merupakan soal jebakan juga, banyak yang mengira kalau soal tersebut menanyakan ∠SQR padahal yang diminta adalah ∠PQS. Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini∠SQR dan ∠PQS merupakan sudut saling berpenyiku, maka:
∠SQR + ∠PQS = 90°
(3x + 5)° + (6x+4)° = 90°
9x° + 9° = 90°
9x° = 81°
x° = 9°
Penyiku ∠SQR = ∠PQS
Penyiku ∠SQR = (6x+4)°
Penyiku ∠SQR = (6.9 + 4)°
Penyiku ∠SQR = 58° (Jawaban D)
Contoh Soal 9
Perhatikan gambar di bawah ini
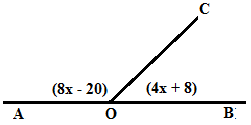
Besar pelurus ∠AOC adalah ….
A. 32°
B. 72°
C. 96°
D. 108°
(UN 2012/2013 paket 5)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠AOC dan ∠BOC merupakan sudut saling pelurus, maka:
∠AOC + ∠BOC = 180°
(8x - 20)° + (4x+8)° = 180°
12x° - 12° = 180°
12x° = 192°
x° = 16°
Pelurus ∠AOC = ∠BOC
Pelurus ∠AOC = (4x+8)°
Pelurus ∠AOC = (4.16 + 8)°
Pelurus ∠AOC = 72° (Jawaban B)
Contoh Soal 10
Perhatikan gambar di bawah ini

Besar penyiku ∠AQC adalah ….
A. 49°
B. 44°
C. 66°
D. 80°
(UN 2012/2013 paket 6)
Penyelesaian:
Untuk menjawab soal ini hal pertama yang Anda cari adalah nilai x. Dalam hal ini ∠AQC dan ∠BQC merupakan sudut saling berpenyiku, maka:
∠AQC + ∠BQC = 90°
(6x + 4)° + (5x+9)° = 90°
11x° + 13° = 90°
11x° = 77°
x° = 7°
Penyiku ∠AQC = ∠BQC
Penyiku ∠AQC = (5x+9)°
Penyiku ∠AQC = (5.7 + 9)°
Penyiku ∠AQC = 44° (Jawaban B)
Demikian contoh soal dan pembahasannya tentang materi garis dan sudut. Semoga artikel ini bermanfaat.
Artikel Terkait
- asd
- asd
- Sinonim akulturasi adalah kontak kabudayaan #sinonim #bahasa #akulturaasi #bahasaindonesia #antonim
- Pada Suatu Pertemuan, Hadir 10 Orang yang Saling Berjabat Tangan. Banyaknya Jabat Tangan yang Terjadi Adalah... Jawaban dan Pembahasan
- Suku Kelima Suatu Barisan Aritmatika Adalah 22, Sedangkan Kesembilan Adalah 42. Suku Kelima Belas Sama Dengan... Jawaban dan Pembahasan
- Mata Uang yang Sering Digunakan Sebagai Alat Pembayaran dan Kesatuan Hitung Dalam Transaksi Ekonomi dan Keuangan Internasional Disebut...
- Kingdom yang Tidak Memiliki Dinding Sel... Jawaban dan Pembahasan
- Organel Sel yang Berperan Untuk Mendetoksifikasi Racun Adalah... Jawaban dan Pembahasan
- Diketahui Harga 4 kg Jeruk, 1 kg Semangka, dan 2 kg Apel Adalah Rp 54.000,00. Harga 1 kg Jeruk, 2 kg Semangka, dan 2 kg Apel Adalah Rp 43.000,00. Sedangkan Harga 3 kg Jeruk, 1 kg Semangka, dan 1 kg Apel Adalah Rp 37.500,00. Berapakah Harga 1 kg Semangka?
- Nilai Rataan Hitung dari Data 4 10 7 x 10 6 11 Adalah 8 Nilai x Adalah ...