Contoh Penyelesaian Soal Trigonometri

Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.

Hubungan fungsi Trigonometri

Fungsi dasar:

Identitas Trigonometri

Rumus Jumlah dan Selisih Sudut

Rumus Perkalian Trigonometri

Baca juga : 

Persamaan Dan Pertidaksamaan Trigonometri

Sudut Istimewa, Pembahasan Dasar dalam Trigonometri

Contoh Soal dan Pembahasan

1. Diketahui salah satu sudut segitiga siku-siku, ABC adalah α . Jika diketahui sin α = 5/15 dan panjang siku siku dihadapan α adalah 15 cm. Hitunglah:

a. Cos α

b. Tan α

Pembahasan : 

a. Sin α = 5/15, jika panjang a= 15 maka berdasarkan rumus  Sin α = a / b , maka panjang b= 45.

Sehingga untuk mendapatkan panjang  b dapat digunakan rumus Segitiga phitagoras.

c² = b² - a²
    = 45² - 15²
    = 2025 - 225
 c =√1800
 c = 30√2

a. Cos α = c/b =  30√2 / 45 = 2 √2 / 3

b. Tan α = a/c = 15 /  30√2 = 1 / 2√2 = 1 / 4√2

 

2. Jika Cos α = 6 /10, tentukan :

a. Sin α

b. Tan α

Pembahasan : 

Sin  α = a / b = 6 / 10, 

Untuk mencari Cos dan Tan, sebelumnya cari dulu panjang c dengan menggunakan Rumus Phytagoras

c² = b² - a²
    = 10² - 6²
    = 100 - 36
 c =√64
 c = 8

a. Cos α = c/b =  8 / 10 

b. Tan α = a/c = 6 / 8

Baca juga : 

Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal

Tips Menghafal Rumus-rumus Trigonometri dengan Cepat dan Mudah

3. Tentukan perbandingan Trigonometri untuk sudut A pada segitiga berikut. Hitunglah nilai Sin A, Cos A, dan Tan A ?

Jika a = 3, c = 5

Pembahasan :

b² = c² - a²
    = 5² - 3²
    = 25 - 9
 b =√16
 b = 4

Sin α = a / c = 3 / 5

Cos α = b / c  =  4 / 5 

Tan α = a / b = 3 / 4

Jika a = 10, c = 26

Pembahasan :

b² = c² - a²
    = 26² - 10²
    = 676 - 100
 b =√576
 b = 24

Sin α = a / c = 10 / 26 

Cos α = b / c = 24 / 26   

Tan α = a / b = 10 / 24

4. Sin 17^o Cos 13^o + Cos 17^o Sin 13^o

Disini kita menggunakan 2 rumus perkalian trigonometri

2SinACosB = Sin(A+B) + Sin(A-B)

dan

2CosASinB = Sin(A+B) - Sin(A-B)

Maka,

Sin 17^o Cos 13^o + Cos 17^o Sin 13^o

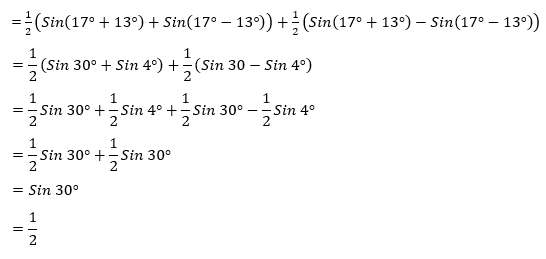
5. Hasil dari

Sin² 10^o + Sin² 20^o + Sin² 30^o+ Sin² 40^o+ Sin² 50^o+ Sin² 60^o+ Sin² 70^o + Sin² 80^o + Sin² 90^o

Pembahasan :

= (Sin² 10^o + Sin² 80^o) + (Sin² 20^o + Sin² 70^o) + (Sin² 30^o + Sin² 60^o) + (Sin² 40^o + Sin² 50^o) + Sin² 90^o

= (Sin² 10^o + Cos² 10^o) + (Sin² 20^o + Cos² 20^o) + (Sin² 30^o + Cos² 30^o) + (Sin² 40^o + Cos² 40^o) + Sin² 90^o  ………..(ingat rumus identitas trigonometri Sin² a + Cos² a = 1)

= 1 + 1 + 1 + 1 +1

= 5

Semangat Belajar ya...