Cara Menghitung Median dan Contoh Soalnya

Dalam belajar matematika tentu anda akan mengenal berbagai istilah serta materi dalam hitungan matematika termasuk salah satunya adalah median atau nilai tengah. Ketika anda dihadapkan pada data yang jumlahnya sangat banyak dan tidak berurutan maka anda akan kesulitan dalam menentukan nilai rata-rata, nilai tengah serta nilai yang paling banyak muncul dari bilangan-bilangan tersebut.

Dari beberapa jenis data tersebut biasanya banyak yang masih kesulitan untuk menentukan nilai tengah dari beberapa bilangan yang ada. Namun anda tak perlu khawatir sebab kini anda bisa menggunakan rumus median untuk data tunggal dan data kelompok yang bisa memudahkan anda dalam menentukan nilai tengah atau median.

Kali ini kita akan mengajak anda membahas topik matematika Median ini secara lengkap dan rinci. Kita akan kupas rumus median ini kemudian kita kerjakan contoh soal supaya mudah dipahami.

Rumus Median untuk Data Tunggal

Median adalah nilai tengah yang berasal dari kumpulan data yang sudah tersusun secara teratur atau sudah diurutkan dari nilai yang terkecil hingga nilai terbesar. Dimana median ini membagi data yang ada menjadi dua bagian sama sehingga bisanya median juga disebut dengan ukuran letak.

Secara matematika median dilambangkan dengan Me untuk menghitung rumus median. Jika terdapat data tunggal maka untuk mencari mediannya maka silakan bedakan terlebih dahulu banyak datanya ganjil dan genap. Bila banyak data ganjil maka Me merupakan data yang letaknya tepat di tengah sesudah anda urutkan.

Namun untuk data genap maka nilai Me adalah rata-rata dari dua data yang letaknya di tengah setelah diurutkan. Untuk memudahkan anda dalam menghitung nilai Me data tunggal baik untuk data ganjil atau genap maka rumus median tersebut yaitu :

Rumus Median Data Tunggal (Ganjil)

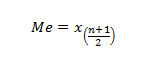
Rumus Median Data Tunggal (Genap)

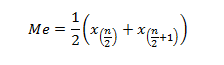
Keterangan :

Me = median

n  = jumlah data

Contoh Soal Median Tunggal

Sepuluh siswa dijadikan sebagai sampel dan dihitung tinggi badannya. Hasil pengukuran tinggi badan sepuluh siswa tersebut dinyatakan dalam data sebagai berikut.

172, 167, 180, 171, 169, 160, 175, 173, 170, 165

Maka hitunglah nilai median data tinggi badan siswa tersebut !

Jawab : Jumlah data tersebut adalah genap maka rumus median yang digunakan adalah rumus untuk data genap dengan cara perhitunganya yaitu :

Me  = ½ ( x n/2 + x ( n/2+ 1) = ½ ( x 10/2 + x (10/2 + 1) = ½ (x₅ + x₆ )

Silakan urutkan data tersebut dari yang terkecil ke yang terbesar

160, 165, 1,67, 169, 170, 171, 172, 173, 175, 180

Diketahui bahwa nilai dari x₅ adalah 170 dan nilai x₆ adalah 171 maka nilai mediannya adalah Me = ½ (170+171) = 170,5.

Rumus Median untuk Data Berkelompok

Pada data tunggal, cara menghitung nilai mediannya memang cukup mudah seperti penjelasan di atas. Namun pada data berkelompok maka data yang digunakan berbentuk kelas interval sehingga anda tidak bisa langsung memperoleh nilai median data tersebut. Untuk itulah rumus median untuk data berkelompok maka dinyatakan sebagai berikut:

Keterangan:

Me = median

xii = batas bawah median

n = jumlah data

fkii = frekuensi kumulatif data di bawah kelas median

fi = frekuensi data pada kelas median

p = panjang interval kelas

 

Contoh Soal Median Data Kelompok

Berikut ini adalah hasil ujian bahasa Inggris kelas XI dari 30 siswa, :

• Yang mendapat nilai 41 – 50, sebanyak 5 orang

• Yang mendapat nilai 51 – 60, sebanyak 8 orang

• Yang mendapat nilai 61 – 70, sebanyak 7 orang

• Yang mendapat nilai 71 – 80, sebanyak 6 orang

• Yang mendapat nilai 81 – 90, sebanyak 4 orang

Berapa nilai median kelompok di atas?

Untuk mencari nilai Median dari Data Kelompok,terlebih dahulu kita menentukan dimana Median itu berada dari Data kelompok diatas, dengan perhitungan:

n / 2

n = Jumlah frekuensi, dalam hal ini frekuensinya adalah jumlah seluruh murid kelas VI, yaitu 30 orang.

n/2 = 30/2 = 15

Jadi Median diketahui berada pada frekuensi yang ke-15, yakni yang mendapat nilai 61-70.

Kemudian kita bisa menentukan Median, dengan rumus:

Median = 60,5 + [{(15 – 13) : (7)} x 10]
Median = 60,5 + {(2 : 7) x 10}
Median = 60,5 + (0,2857 x 10)
Median = 60,5 + 2,857
Median = 63,357

****

Demikianlah penjelasan mengenai rumus median untuk data tunggal dan data berkelompok yang bisa menambah wawasan anda. Bagi anda yang ingin belajar mengenai menghitung median maka silakan ketahui rumusnya sebab untuk data ganjil, genap, tunggal dan kelompok masing-masing memiliki rumus yang berbeda untuk menghitung nilai mediannya.