Cara Cepat Menentukan Invers Suatu Fungsi
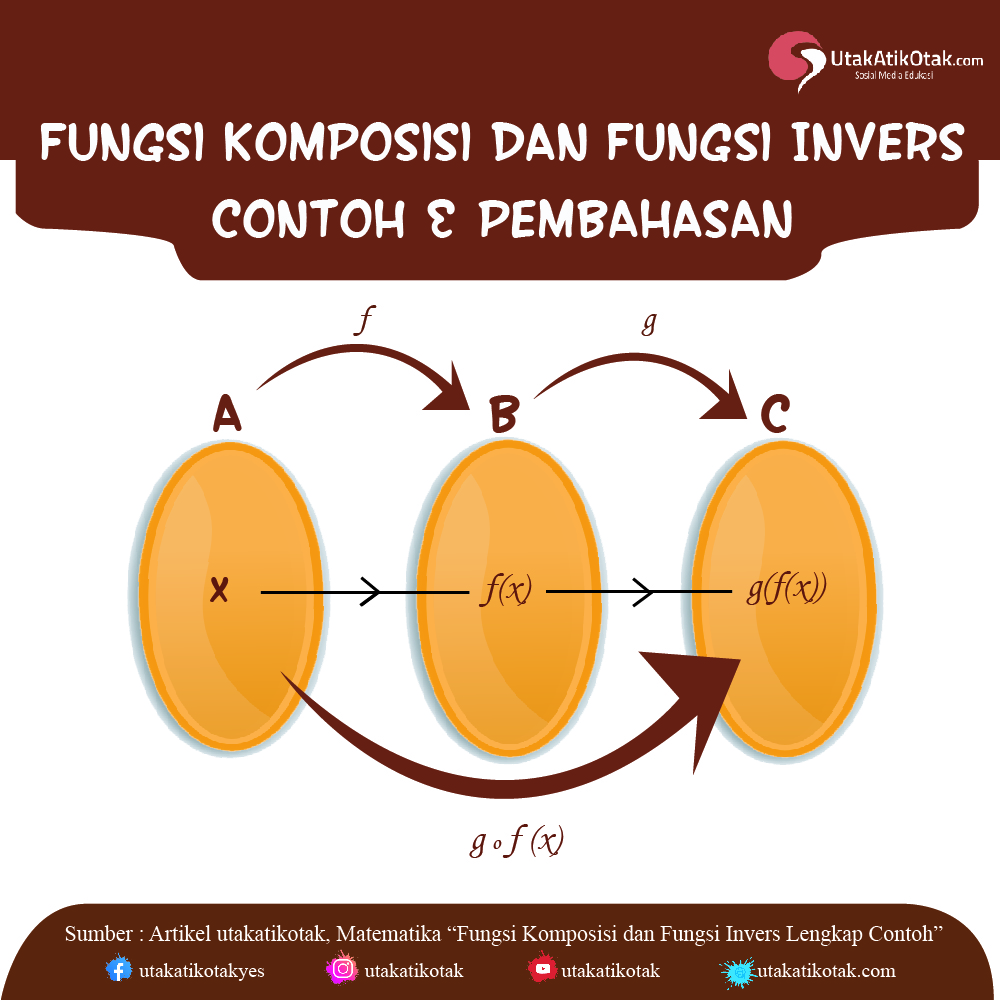
Invers sebuah materi matematika yang diajarkan di kelas XI SMA Semester Genap. Invers suatu fungsi biasanya dilambangkan dengan f-1(x). Menentukan invers fungsi berarti menukar kedudukan antara domain serta kodomain. Apa itu domain dan apa itu kodomain? Domain merupakan daerah asal dan kodomain merupakan daerah hasil. Sehingga bila diketahui fungsi f memetakan dari A ke B maka maka invers fungsi dari f memetakan dari B ke A.
Gambar diatas menunjukan contoh menentukan invers suatu fungsi yaitu fungsi f(x)=2x-1, sehingga didapat invers dari fungsi tersebut yaitu f-1(x)=(x+1)/2
Sebenarnya ada cara alternatif yang dapat dikatakan lebih mudah, berikut ini contoh pengerjaan invers menggunakan cara alternatif dari fungsi f(x)=2x-1
Operasi pada x untuk fungsi f(x)=2x-1 adalah :
- Dikalikan 2
- Dikurangi 1
Kerjakan kebalikan operasi beserta urutannya, maka :
- Ditambah 1
- Dibagi 2
Sehingga inversnya :
Itu contoh yang pertama, perhatikan juga contoh berikutnya
Jika diketahui g(x) = x2 – 4x + 3 maka tentukan g-1(x)!
Penyelesaian :
cara biasa
Misal g(x) = y
cara alternatif
Rubah fungsi g(x)=x²-4x+3 menjadi g(x)=(x-2)²-1 dengan cara melengkapkan kuadrat sempurna.
operasi pada x dari fungsi g(x)=(x-2)²-1, yaitu :
- Dikurangi 2
- Dikuadratkan
- Dikurangi 1
Kerjakan kebalikan operasi beserta urutannya :
- Ditambah 1
- Diakar pangkat dua
- Ditambah 2
Sehingga inversnya menjadi
Menurut sobat semua mudah cara yang mana? cara biasa atau cara alternatif?
Semua terserah sobat yang menggunakannya, namun jika soal yang sobat semua temui bukan pada soal pilihan ganda maka pegajar biasanya meminta cara runtutnya sehingga harus menggunakan cara biasa. Jadi cara alternatif ini dapat dilakukan untuk soal pilihan ganda atau untuk cek apa yang kita kerjakan dengan cara biasa hasilnya benar atau belum.
Baca Juga :
Apa Perbedaan Fungsi Injektif, Surjektif dan Bijektif ?
Pengertian Relasi, Fungsi, Domain,Kodomain dan Range
Fungsi Komposisi dan Fungsi Invers Lengkap dengan Contoh
Agar sobat semua lebih paham, rumus matematika memberikan satu contoh soal lagi.
Tentukan invers dari fungsi F(x) = (2x + 2)2 – 5 ?
Penyelesaian :
Menggunakan Cara biasa
Misalkan F(x) = y
y = (2x + 2)2 – 5
y + 5 = (2x + 2)2
(y + 5)1/2 = 2x + 2
(y + 5)1/2 – 2 = 2x
[(y +5)1/2 – 2]/2 = x
Jadi f-1(x) = [(x + 5)1/2 – 2]/2
Menggunakan cara alternatif/ cara cerdas
operasi x pada fungsi F(x) = (2x + 2)2 – 5 yaitu :
- Dikalikan 2
- Ditambah 2
- Dikuadratkan
- Dikurangi 5
kerjakan kebalikan operaasi beserta urutannya :
- Ditambah 5
- Diakar pangkat 2
- Dikurangi 2
- Dibagi 2
Sehingga hasil inversnya menjadi f-1(x) = [(x + 5)1/2 – 2]/2
Artikel Terkait
- Zat Kimia yang Berfungsi Untuk Menghantarkan Rangsang Listrik Adalah? Jawaban Soal
- Tempat Meyerap Gas Gas Pada Daun
- Alat Kelamin Jantan Pada Bunga Dinamakan
- Fungsi batang pada tumbuhan
- Di dalam tubuh makhluk hidup, beberapa enzim dibentuk dalam keadaan tidak aktif dan diberi nama zimogen. Untuk mengaktifkannya harus dibantu oleh suatu aktivator sehingga berfungsi. Contoh zimogen, aktivator, dan enzim fungsionalnya adalah
- Lapisan pelindung pada daun tumbuhan yang menginspirasi pembuatan lapisan pengilap cat mobil adalah
- Berikut ini, bagian-bagian akar yang dilalui oleh air tanah secara berturut-turut adalah
- Pengendali seluruh kegiatan sel adalah
- Nama organ yang mempunyai peran dalam menyampaikan sel-sel sperma ke dalam organ reproduksi wanita yaitu
- Buah semangka tanpa biji setelah penyerbukan dapat diperoleh dengan memberikan hormon



