Kumpulan Soal dan Pembahasan Bangun Ruang 

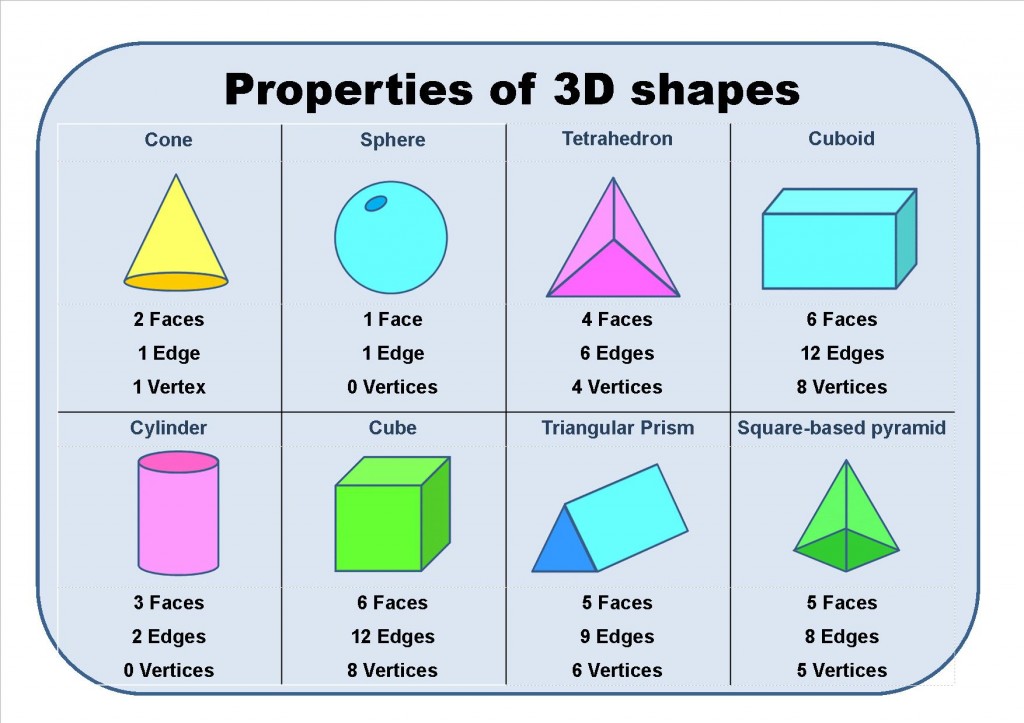
1.     Sebuah kubus memiliki rusuk sepanjang 6 cm. Rusuk itu diperpanjang sebesar k kali panjang rusuk semula, sehingga volumenya menjadi 1.728 cm3 . Nilai k adalah
Jawab:
Skubus semula = 6 cm
Vkubus akhir  = S x S x S
                       = S3
        S            = ∛1.728
                       = 12 cm
Nilai k = 12 cm / 6 cm
           = 2 
Jadi Nilai k adalah 2 kali

Simak Video Berikut ini.

2.    Panjang salah satu diagonal ruang suatu kubus adalah √48 cm3. Volume kubus tersebut adalah
Jawab : 
Klue : - Pertama cari panjang rusuk kubus. Karena yang diketahui adalah Panjang diagonal ruang. Maka kita dapat mencari panjang rusuknya dengan rumus Diagonal Ruang
    Setelah itu cari volume.

P Diagonal Ruang = √(s²+s² + s² )
√48         = √(3s² )
48          = 3S²
S²           = 48/3
S            = √16 
               = 4 cm
Volume = S x S x S
          = (4 x 4 x 4) x cm³ 
          = 64 cm³

 

3.    Rusuk-rusuk balok bertemu pada sebuah balok sebuah pojok balok berbanding 4:4:1 jika volume balok 432 liter, luas permukaan balok adalah
Jawab : 
Klue : - Mencari nilai rusuk balok dengan perbandingan dan volume
          - Mencari luas permukaan balok

Total perbandingan dari volume = 4 x 4 x 1 = 16
R1 = 4/16 x 432 
         = 108 dm

R2 = 4/16 x 432 
         = 108 dm

R3 = 1/16 x 432 
         = 27 dm

R₁ : R₂ : R₃ = 108 : 108 : 27 = 12 : 12 : 3

Luas Permukaan = 2 Luas alas + (Keliling alas x tinggi)
                            = 2 (12 x 12) + (4 x 12 x 3)        (Karena alas berbentuk persegi)
                            = 288 + 144
                            = 432 dm₂
Jadi Luas permukaan adalah sama dengan volume yaitu 432 dm

 

4    Tersedia kawat yang panjangnya 2 m. Bila dibuat balok kerangka yang berukuran 18 cm x 12 cm x 9 cm, Maka sisa kawat yang tak terpakai adalah

Jawab :
Panjang kawat yang tersedia = 2 m = 200 cm
Panjang Kawat Balok yang dibutuhkan
= (4 x panjang) + (4 x lebar) + (4 x tinggi)
= (4 x 18) + (4 x 12) + (4 x 9)
= 72 + 48 + 36
= 156 cm

Sisa kawat = 200 cm – 156 cm = 44 cm

 

5.    Dua buah kubus yang satu berusuk 2 cm dan yang lain berusuk 5 cm. Selisih volume kedua kubus itu adalah 

Jawab :
V1 = S x S x S
      = 2 x 2 x 2
      = 8 cm³
V2 = S x S x S
      = 5 x 5 x 5
      = 125 cm³

Selisih volume = V2 - V1
                        = 125 cm³ - 8 cm³
                        = 117 cm³

 

6.    Sebuah balok memiliki Luas alas 48 cm², Luas sisi samping 30 cm², dan luas sisi depan 40 cm². Volume Balok tersebut adalah

Jawab: 
Luas alas = 48 cm²
p x l         = 48 ................................... persamaan (1)

Luas samping = 30 cm²
l x t          = 30 ............................persamaan (2)

Luas depan = 40 cm²
p x t           = 40..................................persamaan (3)

Mencari Panjang 
Ganti persamaan (1) dan (3)
p x l         = 48  => l = 48/p       ..........persamaan (4)
p x t        = 40  => t = 40/p      ...........persamaan (5)

Isikan ke persamaan (4 & 5) ke persamaan (2)
l x t             = 30
48/p x 40/p =30
1920/p2      = 30
p2               = 1920/30
p2               = 64
p                 = 8 cm

Mencari Lebar dari persamaan (4) 
l = 48/p       
  = 48/8
  = 6 cm
Mencari tinggi dari persamaan (5)
t = 40/p 
  = 40/8
  = 5 cm

Volume = p x l x t
             = (8 x 6 x 5) x cm³
             = 240 cm³

7.   Alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi miring 35 cm dan panjang salah satu sisi siku-sikunya 21 cm. Bila tinggi prisma 20 cm, maka luas sisi prisma adalah

Jawab :
Klue : Mencari sisi siku-siku alas
Sisi tegak = A
A2 = C2 - B2
     = 352 - 212
     = 1225 – 441
     = 784
A  = 28 cm

Luas sisi Prisma = 2 x Luas alas + Keliling alas x tinggi
           = 2 x (1/2 x A x B) + (A + B + C) x tinggi
           = (2 x ½ x 21 x 28) + (28 + 21 + 35) x 20
           = 588 + (84 x 20)
           = 2268 cm2

 

8.    Diketahui panjang seluruh rusuk kubus sama dengan panjang seluruh rusuk balok berukuran 25 cm x 12 cm x 8 cm. Tentukan selisih luas permukaan balok dan kubus !

Jawab :
Rusuk Balok   = (4 x p) + (4 x l) + (4 x t)
        = (4 x 25) + (4 x 12) + (4 x 8)
        = 100 + 48 + 32 
        = 180
Rusuk Kubus = Rusuk Balok = 180
Rusuk Kubus = 12 x sisi
Sisi        = Rusuk Kubus / 12
        = 180 / 12
        = 15 cm

LP Balok = 2 x Luas alas + Keliling alas x tinggi
       = (2 x p x l) + ((2p + 2l) x t)
       = (2 x 25 x 12) + ((50 + 42) x 8)
       = 600 + 736
       = 1336 cm²
LP Kubus = 6 x sisi x sisi
         = 6 x 15 x 15
         = 1350 cm²
Selisih = LP Kubus – LP Balok
    = 1350 – 1336
    = 14 cm²

Baca Juga : 

Soal dan Pembahasan Bangun Ruang Lengkap             

Cara Mudah Menghitung Luas Permukaan Bidang Empat Beraturan

 

9. Sebuah alas Limas beraturan berbentuk persegi dengan panjang 10 cm. Jika tinggi segitiga pada bidang tegakdalamnya adalah 13 cm. Maka hitunglah:
a. Tinggi Limas
b. Luas Permukaan Limas
c. Volume Limas

Jawab:
t.limas = 
           = 
           = 
           = 
           = 12 cm
L.permukaan limas = L.alas + 4 x L.Δ sisi tegak
                           = s² + 4 x  x a Δx t Δ
                           = 10² + 4 x  x 10 x 13
                           = 100 + 2 x 10 x 13
                           = 100 + 260
                           = 360 cm²
volume =  x L.alas x t.limas
            =  x 10² x 12
            = 100 x 4
            = 400 cm³

 

10. Diketahui suatu limas memiliki alas berbentuk persegi, jika luas alas limas 324cm² dan tinggi limas 12cm. berapa luas permukaan limas dan volume limas...?

Jawab:
Sisi = √324
       = 18 cm
18 : 2 = 9 cm

t. Bid Sigak = √12²+9²
                   = √225
                   = 15 cm

Luas Permukaan 
= La + 4 (Bidang Sisi Tegak)
= 324 + 4( 1/2 x 15 x 18)
= 324 + 135
= 459 cm²

Volume = 1/3 x 324 x 12
             = 324 x 4
             = 1296 cm³